人目所見之界,其直線則距等圈之似直線。〈本是圈也人視 為直〉其弧曲線,則亦距等撱圈之半也。以此之故,朔後 三四日,新月之兩端,能過半周之界。
月光日所照與人所見時各不同圖
月光日所照與人所見時《各不同圖說》。
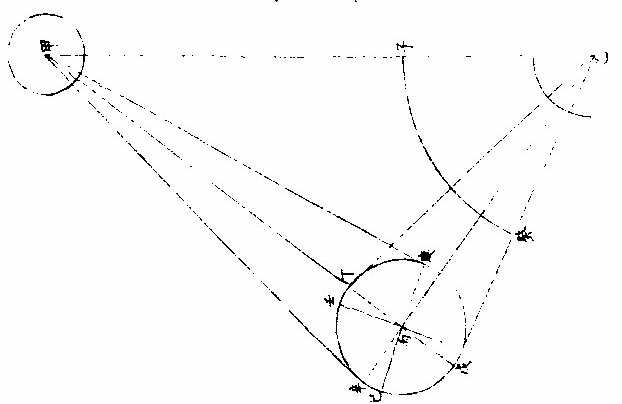
問:「月行每日去離太陽約十二度等也。然朔前後光 魄消長之分數少,兩弦前後消長之分數多,朢前後 復少。人於定朢前後一二日見月光如不易,何故?」曰: 「月禮本圓,圓面之上必有兩圈,皆為明魄之界,一為 日所照之界,一為人所見之界,兩圈於定朔時相合 為一。」〈照與見相反〉定朢時亦合為一。〈照與見相同〉過朔朢,漸相 離。
如兩交圈結於兩極,漸展漸離相離之處,若黃赤二道之距遠度也。
兩界圈之距間,則人所見月體有光之分也。以此推 之,人目所見為球之正面,如平儀之極分交圈也。兩 界合圈,在球之側面,如平儀之子午圈也。初日相離 距度若干,人側視之則見少;如時圈之近子午度分 等,人側視之則見狹。兩弦時距度亦若干,人平視之 則見多,如時圈之近極分圈度分等,人平視之則見 廣也。故朔朢之消長非少而見少,兩弦之消長非多 而見多也。如圖甲為日,乙為地,丙為月,丁丙戊庚為 人所見月之半,己丙庚丁為日所照月之半,丁庚為 兩界之距間,即本時人見月體有光之面也。
從目日及月心,作甲乙丙三角平面平分月體則己丁庚戊為圓面。
甲乙丙角形有甲乙。〈日距地心〉約一千二百地半,徑,有乙、 丙。〈月距地心〉約六十地半徑,又有甲乙丙角,為月距日之 度。〈試作癸子弧即得乙角之度〉求丙甲乙角設月距日之乙角,為 四十度算,得一度五十五分,以并四十度,得四十一 度五十五分。又引長乙丙戊,甲丙辛外角,即與丁丙 庚角等。
庚丁壬丁壬辛,皆四分之一,各減共用之,丁壬,其兩餘等。
甲、丙辛外角與相對之兩內角等,即丁庚弧亦與兩 內角等,則月距日四十度。人所見月體有光之分,約 得四十二度。
言「約」 者,未定之辭也。如上論月體明魄兩界圈似大圈,而實距等圈則有差。又約月距地為六十地半徑,然時多時少,日距地為一千二百地半徑,亦時多時少。又月經度距日四十度,或在南或在北,亦有差,是故約言之。
若測得月體明魄兩界之比例,可推月距日之度,即 上《圖說》反用之。
每日月面光界圖

每日月面《光界圖說》。
欲圖某日之月光界,先求月距太陽若干度分,次依 上法求月面半徑上明魄界若干度分,從兩極。
月面上兩極定為過白道,兩極之大圈線,或與白道為直角。
作撱圈之半,乃本日所見月面有光之界也。若未至 九十度,光作角形,若過九十度,作未成圓形。如圖甲 丙為月之兩極,丁戊為明魄之界,甲戊丙線為本日 之月光界,甲戊丙丁為兩角之形,甲戊丙乙為未成

