割圜密率捷法卷二
- 用法
今之法所以密于古者,以其能用三角形也。然三角形非八线表,不能相求,若一时不得其表,虽精于其法者,亦无从措手。惟用此法,以之立表,则甚以之,推三角形,则不用表,而得数与用表者同,其用可谓溥矣,爰著法数条如左:
- 设圜半径一千万,求四十三度二十一分五十秒之正弦几何
| 一率 |
周天秒 |
一二九六〇〇〇 |
|
| 二率 |
倍圜周定率 |
六二八三一八五三 |
|
| 三率 |
角度化秒 |
一五六一一〇 |
|
| 四率 |
弧背 |
七五六八四二六 |
三
|
|
| 左
|
| 七二二五四五|八
|
第二条
|
| 二八二|〇
|
第四条
|
| 七二二八二七|八
|
|
|
| 右
|
| 七五六八四二六|三
|
第一条
|
| 二〇六九四|〇
|
第三条
|
| 二|二
|
第五条
|
| 七五八九一二二|五
|
|
|
| 七五八九一二二|五
|
| 七二二八二七|八
|
| 六八六六二九四|七
|
|
|
|
|
|
法以周天度化为一百二十九万六千秒,为一率;倍圜周定率〈通径设为二千万,倍于定率,故圜周定率亦倍之〉得六千二百八十三万一千八百五十三,为二率;设度化为一十五万六千一百一十秒,为三率,乘除得四率七百五十六万八千四百二十六〈小馀三,带小馀一位单位数方密,后仿此〉,为弧背〈角度为旋转一周之虚数,弧背为半径上圜周之曲线〉,为第一条,书右;次以半径一千万为连比例第一率,第一条〈即弧背〉为连比例第二率,乘除得连比例第三率五百七十二万八千一百零七,为比例常用之数;次置第一条,以三率乘之,一率除之,得四率数,六除之〈与二除之又三除之同〉,得七十二万二千五百四十五〈八〉,为第二条,书左;次置第二条,以三率乘之,一率除之,得六率数,二十除之〈与四除之又五除之同,馀仿此〉,得二万零六百九十四,为第三条,书右;次置第三条,以三率乘之,一率除之,得八率数,四十二除之,得二百八十二,为第四条,书左〈每次得数降二位,第四条数尚有三位,须求第五条数〉;次置第四条,以三率乘之,一率除之,得十率数,七十二除之,得二〈二〉,为第五条,书右〈第五条数止一位,第六条数必在小馀下,故可省求〉;次并右三条,得总数七百五十八万九千一百二十二〈五〉,并左二条,得总数七十二万二千八百二十七〈八〉,置右总数减左总数得六百八十六万六千二百九十五〈小馀七进为一。在旧法当一减、一加累求之,今以应加者书右,应减者书左,只用加二次、减一次,较为省便〉,即四十三度二十一分五十秒之正弦线也。
| 一率 |
周天秒 |
一二九六〇〇〇 |
|
| 二率 |
倍圜周定率 |
六二八三一八五三 |
|
| 三率 |
较度化秒 |
五八九〇 |
|
| 四率 |
较弧背 |
二八五五五五 |
二
|
|
|
|
| 右
|
| 二八五五五五|二
|
第一条
|
| 三八|八
|
|
| 二八五五一六|四
|
较弧正弦
|
|
|
|
| 四〇七七|〇
|
第一条
|
| 〇|二
|
|
| 四〇七六|八
|
较弧正矢
|
|
|
| 一率 |
半径 |
一〇〇〇〇〇〇〇 |
|
| 二率 |
借弧正弦 |
七〇七一〇六八 |
|
| 三率 |
较弧正弦正矢和 |
二八九五九三 |
二
|
| 四率 |
正弦较 |
二〇四七七三 |
|
|
|
|
|
|
又法借四十五度,与所设弧度相减,馀一度三十八分十秒,为较度,化秒比例得较弧背二八五五五五〈二〉。先求正弦,以弧背为第一条书右;次以半径为连比例第一率,第一条为连比例第二率,求得连比例第三率八一五四,为连比例常用之数;次置第一条,以三率乘之,一率除之,得四率数,六除之,得三八〈八〉,为第三条,书左〈第二条得数仅二位,而比第一条数降四位,则第三条数必降至奇零下,即无庸求〉,左右二条相减,得二八五五一六〈四〉,为较弧正弦;次求正矢,置前得第三率之数,二除之,得四〇七七,为第一条,书右;次置第一条,以三率乘之,一率除之,得五率数,十二除得小馀〈二〉,为第二条,书左,左右二条相减,得四〇七六〈八〉,为较弧正矢次,以半径一〇〇〇〇〇〇〇为一率,四十五度正弦七〇七一〇六八为二率,较弧正弦正矢相加〈设弧于借弧故加〉,得二八九五九三〈二〉,为三率,乘除得四率二〇四七七三,为正弦较,与四十五度正弦七〇七一〇六八相减,馀六八六六二九五,为设弧正弦,与前得数相同。
- 设圜半径一千万,求四十三度二十一分五十秒之馀弦几何
| 左
|
| 一三六七一三|三
|
第二条
|
| 二六|七
|
第四条
|
| 一三六七四〇|〇
|
|
|
| 右
|
| 二八六四〇五三|五
|
第一条
|
| 二六一〇|三
|
第三条
|
| |一
|
第五条
|
| 二八六六六六四|〇
|
|
|
| 二八六六六六四
|
|
| 一三六七四〇
|
|
| 二七二九九二四
|
正矢
|
| 一〇〇〇〇〇〇〇
|
|
| 七二七〇〇七六
|
馀弦
|
|
|
|
|
法用周天秒及圜周定率比例得弧背〈法数俱见前题〉,次以圜半径为连比例第一率,弧背为连比例第二率,求得第三率〈数见前〉,二除之,得二八六四〇五三〈五〉,为第一条,书右;次置第一条,以三率乘之,一率除之,得五率数,十二除之,得一三六七一三〈三〉,为第二条,书左;次置第二条,以三率乘之,一率除之,得七率数,三十除之,得二六一〇〈三〉,为第三条,书右;次置第三条,以三率乘之,一率除之,得九率数,五十六除之,得二六〈七〉,为第四条,书左;次置第四条,以三率乘之,一率除之,得十一率数,九十除之,得小馀〈一〉,为第五条,书右;次并右三条得总数二八六六六六四,并左二条得总数一三六七四〇,置右总数减左总数,得二七二九九二四,为四十三度二十一分五十秒之正矢,与半径相减,得七二七〇〇七六,即所求之馀弦也。
| 一率 |
半径 |
一〇〇〇〇〇〇〇 |
|
| 二率 |
借弧馀弦 |
七〇七一〇六八 |
|
| 三率 |
较弧正弦正矢较 |
二八一四三九 |
六
|
| 四率 |
馀弦较 |
一九九〇〇七 |
八
|
|
| 七〇七一〇六八|
|
| 一九九〇〇七|八
|
| 七二七〇〇七五|八
|
|
|
|
又法借四十五度与所设度相减,得较弧,度、分、秒比例得较弧弧背,求得正弦及正矢〈数俱见前题〉,及以半径为一率,四十五度馀弦七〇七一〇六八为二率,较弧正弦、正矢相减,得二八一四三九〈六〉,为三率,乘除得四率一九九〇〇七〈八〉,与四十五度馀弦相加,得七二七〇〇七六,即设弧馀弦,与前得数同。
- 设圜半径一千万,求四十六度三十八分十秒之正弦几何
法以所设弧度、分、秒与象限九十度相减,馀四十三度二十一分五十秒,为馀弧,以馀弧求得正矢〈法数俱见前题〉,与半径相减得七二七〇〇七六,即设弧之正弦也。
又法借四十五度,与所设度相减,馀一度三十八分十秒,为较弧,以较弦求得正弦、正矢;次以半径为一率,四十五度正弦为二率,较弧正弦、正矢相减馀为三率,求得四率,为正弦较,与四十五度正弦相加,得七二七〇〇七六,即设弧之正弦也〈法数俱与前题求馀弦同〉。
- 设圜半径一千万,求四十六度三十八分十秒之馀弦几何
法以所设度、分、秒与象限九十度相减,馀四十三度二十一分五十秒,为馀弧,以馀弧求得正弦六八六六二九五,即设弧之馀弦也〈法数俱见前题〉。
又法求得设弧,与四十五度较弧之正弦、正矢,次以半径为一率,四十五度馀弦为二率,较弧正弦、正矢相加为三率,乘除得四率,与四十五度馀弦相减,得六八六六二九五,即设弧久馀弦也〈法数俱与前题求正弦同〉。
- 设甲乙丙直线三角形,甲乙边一丈八尺七寸三分,甲角七十四度,乙角六十二度,求馀二边一角各几何

|
| 一率 |
周天度 |
三六〇 |
|
| 二率 |
倍圜周率 |
六二八三一八 |
五三
|
| 三率 |
乙角馀度 |
二八 |
|
| 丙角度 |
四四 |
|
| 四率 |
乙角馀弧背 |
四八八六九 |
二
|
| 丙角弧背 |
七六七九四 |
五
|
|
|
|
| 右
|
| 一一九四〇|八
|
第一条
|
| 一|八
|
第三条
|
| 一一九四二|六
|
|
|
| 一一九四二|六
|
|
| 二三七|六
|
|
| 一一七〇五|〇
|
乙馀角正矢
|
| 一〇〇〇〇〇
|
|
| 八八二九五
|
乙角正弦
|
|
| 七五四八|一
|
第二条
|
| 三|一
|
第四条
|
| 七五五一|二
|
|
|
| 七六七九四|五
|
第一条
|
| 二二二|五
|
第三条
|
| 七七〇一七|〇
|
|
|
| 七七〇一七|〇
|
|
| 七五五一|二
|
|
| 六九四六五|八
|
丙角正弦
|
|
|
| 一率 |
半径
|
| 二率 |
乙角正弦
|
| 三率 |
甲乙
|
| 四率 |
甲辛
|
|
| 一率 |
丙角正弦
|
| 二率 |
半径
|
| 三率 |
甲辛
|
| 四率 |
甲丙
|
|
|
|
如图:甲乙丙形,有甲乙边及甲乙二角,求馀二边、一角。先并二角,与半周相减,得丙角四十四度;次以圜周度与倍圜周率比例,得乙角馀弧背四八八六九〈二〉、丙角弧背七六七九四〈五〉,命半径为十万,求得乙馀角正矢一一七〇五与半径相减,馀八八二九五,为乙角正弦〈丁戊〉,求得丙角正弦〈己庚〉六九四六五〈八〉;次以半径〈乙丁〉为一率,乙角正弦〈丁戊〉为二率,甲乙边为三率,求得四率一丈六尺五寸三分七釐六毫为中垂线〈甲辛〉;次以丙角正弦〈己庚〉为一率,半径〈己丙〉为二率一中垂线〈甲辛〉为三率,求得四率二丈三尺八寸零六釐八毫为甲丙边;次以中垂线〈甲辛〉为股,甲乙边为弦,求得勾八尺七寸九分三釐二毫,为小分底〈乙辛〉;又以中垂线〈甲辛〉为股,甲丙边为弦,求得勾一丈七尺一寸二分五釐二毫为大分底〈丙辛〉,并二分底得二丈五尺九寸一分八釐四毫,为乙丙边。
- 设甲乙丙直线三角形,甲丙边二丈三尺八寸零六釐八毫,乙丙边二丈五尺九寸一分八釐四毫,丙角四十四度,求馀二角一边各几何

|
| 左
|
| 一四四九|一
|
第二条
|
| |三
|
第四条
|
| 一四四九|四
|
|
|
| 右
|
| 二九四八七|〇
|
第一条
|
| 二八|四
|
第三条
|
| 二九五一五|四
|
|
|
| 二九五一五|四
|
|
| 一四四九|四
|
|
| 二八〇六六|〇
|
丙角正矢
|
| 一〇〇〇〇〇
|
|
| 七一九三四|〇
|
丙角馀弦
|
|
|
| 一率 |
半径
|
| 二率 |
丙角馀弦
|
| 三率 |
甲丙
|
| 四率 |
丙辛
|
|
| 一率 |
甲乙
|
| 二率 |
乙辛
|
| 三率 |
半径
|
| 四率 |
乙角馀弦
|
|
| 四六九四七|一
|
第一条
|
| 一七二四|五
|
第二条
|
| 一七一|〇
|
第三条
|
| 二二|四
|
第四条
|
| 三|三
|
第五条
|
| |五
|
第六条
|
| 四八八六八|八
|
|
|
|
|
法先比例得丙角弧背〈见前题〉,求得正矢二八〇六六,与半径相减,得七一九三四为丙角馀弦〈丙庚〉;次以半径〈丙己〉为一率,丙角馀弦〈丙庚〉为二率,甲丙边为三率,求得四率一丈七尺一寸二分五釐二毫为大分底〈丙辛〉,与乙丙边相减馀八尺七寸九分三釐二毫为小分底〈乙辛〉;次以甲丙边自乘,大分底〈丙辛〉、小分底〈乙辛〉和较相乘,二积相减馀数开平方得一丈八尺七寸三分为甲乙边〈两分底和较相乘之积与两腰和较相乘之积等,亦即与两腰方相较之积等,故大腰自乘之积内减分底和较相乘之积,馀即小腰自乘之积也〉;次以甲乙边为一率,小分底〈乙辛〉为二率,半径〈乙丁〉为三率,求得四率四六九四七〈一〉,为乙角馀弦〈乙戊〉;次按以乙角馀弦为乙馀角正弦用正弦求弧背法,求得弧背四八八六八〈八〉,以一度之弧背数一七四五三〈三〉除之馀,得二十八度,为乙馀角度,与九十度相减得六十二度,即乙角度;次并乙、丙二角,与半周相减,得七十二度为甲角度。
- 设黄赤大距二十三度二十九分,太阳黄道实行酉宫十度,问赤道同升度及距纬度各几何

|
| 一率 |
周天分
|
| 二率 |
倍圜周率
|
| 三率 |
大距分
|
| 四率 |
大距弧背
|
|
| 一率 |
周天度
|
| 二率 |
倍圜周率
|
| 三率 |
黄道度
|
| 四率 |
黄道弧背
|
|
| 左
|
| 一一四七五一|九
|
第二条
|
| 三|八
|
第四条
|
| 一一四七五五|七
|
|
|
| 右
|
| 四〇九八六一四|八
|
第一条
|
| 九六三|八
|
第三条
|
| 四〇九九五七八|六
|
|
|
| 四〇九九五七八|六
|
|
| 一一四七五五|七
|
|
| 三九八四八二二|九
|
大距正弦
|
|
| 五六七一〇一|五
|
第二条
|
| 一六〇|三
|
第四条
|
| 五六七二六一|八
|
|
|
| 六九八一三一七|〇
|
第一条
|
| 一三八一九|九
|
第三条
|
| 一|〇
|
第五条
|
| 六九九五一三七|九
|
|
|
| 六九九五一三七|九
|
|
| 五六七二六一|八
|
|
| 六四二七八七六|一
|
黄道正弦
|
|
|
| 一率 |
半径
|
| 二率 |
大距正弦
|
| 三率 |
黄道正弦
|
| 四率 |
距纬正弦
|
|
| 三五六一三九四|八
|
第一条
|
| 二八〇〇七|七
|
第二条
|
| 八二六|八
|
第三条
|
| 三二|二
|
第四条
|
| 一|四
|
第五条
|
| 二五九〇二六二|九
|
距纬弧背
|
|
| 一率 |
距纬馀弦
|
| 二率 |
壬辛线
|
| 三率 |
半径
|
| 四率 |
赤道正弦
|
|
| 七〇七一〇六七|八
|
|
| 六〇九九九五五|九
|
|
| 〇九七一一一一|九
|
正弦较
|
|
| 七九二四八一七|七
|
|
| 七〇七一〇六七|八
|
|
| 〇八五三七四九|九
|
馀弦较
|
|
| 一三九三七八九|三
|
第一条
|
| 九〇二|三
|
第二条
|
| 一|六
|
第三条
|
| 一二九四六九三|二
|
较弧背
|
|
|
|
如图〈取浑圜八分之一〉:甲乙丙正弧三角形,甲丁为黄道,甲戊为赤道,甲为春分,甲角为交角,即丁戊大距度,丁己为半径,丁庚为正弦,乙为太阳,甲乙为大阳距春分黄道度四十度,甲丙为距春分赤道度,乙丙为距纬,乙辛为黄道正弦,乙壬为距纬正弦,自壬至辛联辛壬线成乙辛壬勾股形,与丁己庚勾股形为同式形,丙癸为赤道正弦,丙己癸与壬己辛亦为同式勾股形。法先比例得大距弧背〈丁戊〉四〇九六一四〈八〉、黄道弧背〈甲乙〉六九八一三一七,求得大距正弦〈丁庚〉二九八四八二三、黄道正弦〈乙辛〉六四二七八七六;次以半径〈丁己〉为一率,大距正弦〈丁庚〉为二率,黄道正弦〈乙辛〉为三率,求得四率二五六一三九五为距纬正弦〈乙壬〉;次按正弦求弧背法,求得二五九〇二六二〈九〉为距纬弧背,以一秒之弧背四八〈四八一三六八〉除之,得五三四二八为距纬秒数,递以六十进之,得十四度五十分二十八秒即太阳距赤道北之纬度;次以半径〈乙己〉为弦,距纬正弦〈乙壬〉为股,求得勾九六六六三九八为距纬馀弦〈己壬〉,又以黄道正弦〈乙辛〉为弦,距纬正弦〈乙壬〉为股,求得勾五八九五四九三六为壬辛线;次以距纬馀弦〈己壬〉为一率,壬辛线为二率,半径〈丙己〉为三率,求得四率六〇九八九五五〈九〉为赤道正弦〈丙癸或以半径距纬正弦和较相乘为一率,黄道正弦距纬正弦和较相乘为二率,半径自乘为三率,求得四率为赤道正弦自乘方,开平方得赤道正弦〉;次用借弦求弧背法,以赤道正弦与四十五度正弦相减,馀九七一一一一〈九〉为股,求得赤道馀弦〈己癸〉七九二四八一七〈七〉,与四十五度馀弦相减馀八五三七四九〈九〉为勾,求得弦一二九三七八九〈三〉为较通弦,用通弦求弧背法求得一二九四六九三〈二〉为较弧背,以一秒之弧背数除之得数,以六十递进之,得七度二十五分零五秒为较弧度,与四十五度相减,得三十七度三十四分五十五秒为距分赤道度,加春分距冬至九十度,满三十度进一宫,为酉宫零七度五十四分五十五秒,即太阳赤道同升也。
- 设金星黄道经度午宫十度五十五分纬北六度四十四分,黄赤大距二十三度二十九分,问赤道经纬度各几何

|
|
|
|
| 右
|
| 六九〇五三|三七
|
第一条
|
| |〇三
|
第三条
|
| 六九〇五三|四〇
|
|
|
| 六九〇五三|四〇
|
|
| 七九|七二
|
|
| 六八九七三|六八
|
|
| 一〇〇〇〇〇〇〇|〇〇
|
|
| 九九三一〇二六|三二
|
丁辛弧正弦
|
|
| 六〇六九八九|九
|
第二条
|
| 一八七|九
|
第四条
|
| 六七一七七|八
|
|
|
| 七一四一三〇五|五
|
第一条
|
| 一五四七五|七
|
第三条
|
| 一|三
|
第五条
|
| 七一五六七八二|五
|
|
|
| 七一五六七八二|五
|
|
| 六〇七一七七|八
|
|
| 六五四九六〇四|七
|
丁角正弦
|
|
|
| 一率 |
半径〈壬卯〉
|
| 二率 |
丁角正弦〈壬寅〉
|
| 三率 |
丁辛正弦〈辛丑〉
|
| 四率 |
辛子正弦〈辛辰〉
|
|
|
|
| 一〇〇〇〇〇〇〇
|
|
| 九八八〇一三九
|
|
| 〇〇一一九八六一
|
馀矢
|
| 二
|
|
| 二三九七二二|〇
|
第一条
|
| 四七八|九
|
第二条
|
| 一|五
|
第三条
|
| 二四〇二〇二|四
|
三率
|
|
|
|
|

|
| 左
|
| 四二四一四|二
|
第二条
|
| 二|六
|
第四条
|
| 四二四一六|八
|
|
|
| 右
|
| 一五九五二五九|〇
|
第一条
|
| 四五一|一
|
第三条
|
| 一五九五七一〇|一
|
|
|
| 一五九五七一〇|一
|
|
| 四二四一六|八
|
|
| 一五五三二九三|三
|
馀弧正矢
|
| 一〇〇〇〇〇〇〇
|
|
| 八四四六七〇六|七
|
甲子弧正弦
|
|
|
| 一率 |
半径〈子卯〉
|
| 二率 |
垂弧距赤极正弦〈子午〉
|
| 三率 |
垂弧馀弦〈卯辰〉
|
| 四率 |
辰未线
|
|
| 八六三八四六
|
星距赤极馀矢
|
| 二
|
|
| 一七二七六九二|〇〇
|
第一条
|
| 二四八七四|三三
|
第二条
|
| 五七三|〇〇
|
第三条
|
| 一五|九一
|
第四条
|
| |四九
|
第五条
|
| 一七五三一五五|七三
|
三率
|
|
|
|
|
| 一率 |
星距赤极正弦〈辛未〉
|
| 二率 |
垂弧正弦〈辛辰〉
|
| 三率 |
半径〈癸卯〉
|
| 四率 |
星距夏至赤道正弦〈癸申〉
|
|
| 七一一九四四〇
|
|
| 七〇七一〇六八
|
|
| 〇〇四八三七二
|
正弦较
|
|
| 七〇七一〇六八
|
|
| 七〇二三〇七四
|
|
| 四七九九四
|
馀弦较
|
|
|
|
| 六八一四一|六
|
第一条
|
| |一
|
第二条
|
| 六八一四一|七
|
弧背较
|
|
|
|
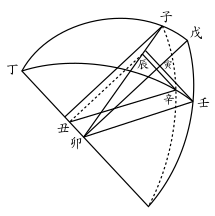
如图:甲为赤极,乙丙为赤道,丁为黄极,戊己为黄道,己为冬至,戊为夏至,庚为秋分,辛为金星,成甲丁辛斜弧三角形,甲丁为二极相距,丁辛为星距黄极,甲辛为星距赤极,丁角为星距夏至,黄道经度当戊壬弧,甲角为星距赤道,经度当丙癸弧,此形有甲丁、丁辛二边及丁角,求甲辛边及甲角自秋分庚点作庚子象限弧。辛子为形外垂弧。用丁辛子、甲辛子二正弧三角形算之,先用丁辛子形,如第二图比例,得丁辛星距黄极之馀弧背〈即辛壬星距黄道北纬度之弧背〉一一七五一八八三〈三〉,求得正矢六八九七四,与半径相减得九九三一〇二六,为丁辛星距黄极之正弦〈辛丑〉,又比例得丁角星距夏至黄道弧背七一四一三〇五〈五〉,求得正弦〈壬寅〉六五四九六〇五;次以半径〈壬卯〉为一率,丁角正弦〈壬寅〉为二率,丁辛正弦〈辛丑〉为三率,求得四率六五〇四四三〇为垂弧正弦〈辛辰〉,次用辛子辰勾股形,有辛丑弦、辛辰股,求得丑辰勾七五〇四五一〇;次以垂弧馀弦〈卯辰〉为一率,丑辰为二率,半径〈子卯〉为三率,求得四率九八八〇一三九,为垂弧距黄极〈丁子〉之正弦〈子己〉;次以垂弧距黄极之正弦与半径相减,馀一一九八六一为馀矢,按正矢求弧背法,求得弧背一五四九八四六,以一秒之弧背除之,得三一九六八,满六十递进之,得八度五十二分四十八秒为馀弧,与九十度相减,得八十一度零七分一十二秒为垂弧,距黄极〈丁子〉与二极相距度〈甲丁〉相减,得五十七度三十八分一十二秒为垂弧距赤极〈甲子〉,如第三图,以甲子之馀度三十二度二十一分四十八秒比例得弧背五六四八四六七〈二〉,求得正矢一五五三二九三〈三〉,与半径相减得八四四六七〇六〈七〉,为垂弧距赤极之正弦〈子午〉;次以半径〈子卯〉为一率,垂弧距赤极正弦〈子午〉为二率,垂弧馀弦〈卯辰〉为三率,求得四率六四一五七三九,为辰未线;次以辰未为勾,辛辰为股,求得辛未弦九一三六一五四为星距赤极正弦,以正弦与半径相减,馀八六三八四六为星距赤极馀矢,按正矢求弧背法,求得弧背四一八七〇七〇,以一秒之弧背除之,得八六三六四〈五〉为秒数,递以六十进之,得二十三度五十九分二十四秒半为星距赤极馀度,即星距赤道北纬度〈辛癸〉,与象限九十度相减,得六十六度零三十五秒半,为星距赤极〈甲辛〉;次以星距赤极正弦〈辛未〉为一率,垂弧正弦〈辛辰〉为二率,半径〈癸卯〉为三率,求得四率七一一九四四〇,为星距夏至赤道正弦〈癸申〉,随求得馀弦〈卯申〉七〇二三〇七四,用借弦求弧背法,借四十五度之正弦、馀弦,减得正弦较四八三七二、馀弦较四七九九四,求得较弧通弦六八一四一〈六〉;次按通弦求弧背法,求得较弧背六八一四一〈七〉,以一秒之弧背除之,得一四〇五〈五〉,为秒数,满六十进之,得二十三分二十五秒半,与借弧四十五度相加,满三十度进一宫,得一宫十五度二十三分二十五秒半,为星距夏至赤道宫度,加夏至距冬至六宫,得七宫为午宫十五度二十三分三十五秒半,即金星赤道经度也。
- 设金星黄道北纬度六度四十四分,赤道北纬度二十三度五十九分二十四秒三十微,黄赤大距二十三度二十九分,问黄道经度赤道经度各几何

|
| 左
|
| 四一六四一|三
|
第二条
|
| |三
|
第四条
|
| 四一六四一|六
|
|
|
| 右
|
| 二九二三四二六|五
|
第一条
|
| 三一七七|九
|
第三条
|
| 二九二三六〇四|四
|
|
|
| 二九二三六〇四|四
|
|
| 四一六四一|六
|
|
| 二八八一九六二|八
|
总弧馀弦
|
|
| 二四四四六七|一
|
第二条
|
| 二二|三
|
第四条
|
| 二四四四八九|六
|
|
|
| 五二七三八〇三|二
|
第一条
|
| 三三九九|六
|
第三条
|
| 五二七七二〇二|八
|
|
|
| 五二七七二〇二|八
|
|
| 二四四四八九|六
|
|
| 五〇三二七一三|二
|
较弧馀弦
|
|
| 一二二三四二|九
|
第二条
|
| 四|四
|
第四条
|
| 一二二三四七|三
|
|
|
| 四一八七〇六九|一
|
第一条
|
| 一〇七二|四
|
第三条
|
| 四一八八一四一|五
|
|
|
| 四一八八一四一|五
|
|
| 一二二三四七|三
|
|
| 四〇六五七九四|二
|
星距赤极馀弦
|
|
| 二八八一九六二|八
|
总弧馀弦
|
| 五〇三二七一三|二
|
较弧馀弦
|
| 七九一四六七六|〇
|
|
| 三九五七三三八
|
中数
|
|
| 五〇三二七一三|二
|
较弧馀弦
|
| 四〇六五七九四|二
|
星距赤极馀弦
|
| 〇九六六九一九|〇
|
矢较
|
|
|
| 一率 |
中数〈午未〉
|
| 二率 |
矢较〈戌辛〉
|
| 三率 |
半径〈戊庚〉
|
| 四率 |
丁角正矢〈戊壬〉
|
|
| 二四四三三五七|一二
|
正矢
|
| 二
|
|
| 四八八六七一四|二四
|
第一条
|
| 一九八九九九|八〇
|
第二条
|
| 一二九六六|〇六
|
第三条
|
| 一〇一八|三
|
第四条
|
| 八八|四六
|
第五条
|
| 八|一九
|
第六条
|
| |七九
|
第七条
|
| 五〇九九七九五|八
|
三率
|
|
|
|
|
| 一率 |
甲辛正弦
|
| 二率 |
丁角正弦
|
| 三率 |
丁辛正弦
|
| 四率 |
甲角正弦
|
|
|
|
如图:以星距黄极〈丁辛〉与二极相距〈甲丁〉相加,得一百零六度四十五分,为总弧〈甲子〉,相减得五十九度四十七分,为较弧〈甲丑〉,比例得丙子〈总弧减去象限〉弧背二九二三四二六〈五〉,求得正弦〈子寅〉二八八一九六三为总弧馀弦,比例得乙丑〈甲丑之馀〉弧背五二七三八〇三〈二〉,求得正弦〈丑卯〉五〇三二七一三,为较弧馀弦,以两馀弦相加,得七九一四六七六〈子辰〉,折半得三九五七三三八〈辰巳与午未等〉为中数,为一率,比例得辛癸〈甲辛之馀〉弧背四一八七〇六九〈一〉,求得正弦〈辛申〉四〇六五七九四,为星距赤极馀弦,与较弧馀弦〈丑卯〉相减,馀九六六九一九为矢较〈丑酉与戌辛等〉,为二率,半径〈戊庚〉为三率,求得四率二四四三三五七〈一二〉,为星距夏至黄道正矢〈戊壬〉,求得弧背七一四一二八五〈五〉,以一秒之弧背除之,得一四七三〇〇为秒数,收作一宫十度五十五分,为星距夏至黄道度,加六宫,得七宫,为午宫十度五十五分为金星黄道经度〈矢较比例之理详见考成上编〉;次以星距赤极〈甲辛〉正弦为一率,星距夏至黄道经度〈丁角〉正弦为二率,星距黄极〈丁辛〉正弦为三率,求得四率七一一九四三九,为星距夏至赤道经度〈甲外角〉正弦,求得弧背秒数收作一宫十五度二十三分二十五秒半〈各数俱见前题〉,加六宫,得七宫为午宫十五度二十三分二十五秒半,即金星赤道经度也。
割圜密率捷法卷二终
本清朝作品在全世界都属于公有领域,因为作者逝世已经超过100年。
Public domainPublic domainfalsefalse






