GB 3102.11-1993 物理科学和技术中使用的数学符号

中华人民共和国国家标准
物理科学和技术中使用的数学符号
Mathematical signs and symbols for use in the physical sciences and technology
GB 3102.11-1993
1993年12月

本作品收录于《GB 3102 量和单位》

替代 GB 3102.11-1986，1994年7月1日起实施

引言

本标准等效采用国际标准 ISO 31-11:1992《量和单位　第十一部分：物理科学和技术中使用的数学标志与符号》。

本标准是目前已经制定的有关量和单位的一系列国家标准之一，这一系列国家标准是：

GB 3100　国际单位制及其应用；

GB 3101　有关量、单位和符号的一般原则；

GB 3102.1　空间和时间的量和单位；

GB 3102.2　周期及其有关现象的量和单位；

GB 3102.3　力学的量和单位；

GB 3102.4　热学的量和单位；

GB 3102.5　电学和磁学的量和单位；

GB 3102.6　光及有关电磁辐射的量和单位；

GB 3102.7　声学的量和单位；

GB 3102.8　物理化学和分子物理学的量和单位；

GB 3102.9　原子物理学和核物理学的量和单位；

GB 3102.10　核反应和电离辐射的量和单位；

GB 3102.11　物理科学和技术中使用的数学符号；

GB 3102.12　特征数；

GB 3102.13　固体物理学的量和单位。

上述国家标准贯彻了《中华人民共和国计量法》、《中华人民共和国标准化法》、国务院于 1984 年 2 月 27 日公布的《关于在我国统一实行法定计量单位的命令》和《中华人民共和国法定计量单位》。

本标准的特殊说明：

变量（例如 𝑥, 𝑦 等）、变动附标（例如 ∑_𝑖𝑥_𝑖 中的 𝑖）及函数（例如 𝑓, 𝑔 等）用斜体字母表示。点 𝐴、线段 𝐴𝐵 及 弧 𝐶𝐷 用斜体字母表示。在特定场合中视为常数的参数（例如 𝑎, 𝑏 等）也用斜体字母表示。

有定义的已知函数（例如 sin，exp，ln，Γ 等）用正体字母表示。其值不变的数学常数（例如 e = 2.718 281 8…，π = 3.141 592 6…，i² = −1 等）用正体字母表示。已定义的算子（例如 div，δ𝑥 中的 δ 及 d𝑓/d𝑥 中的 d）也用正体字母表示。

数字表中数（例如 351 204，1.32，7/8）的表示用正体。

函数的自变量写在函数符号后的圆括号中，且函数符号与圆括号之间不留空隙，例如 𝑓(𝑥), cos(𝜔𝑡 + 𝜑)。如果函数的符号由两个或更多的字母组成且自变量不含 +, −, ×, ⋅ 或 / 等运算时，括于自变量的圆括号可以省略，这时在函数与自变量符号之间应留一空隙，例如 ent 2.4，sin 𝜔𝑡，arcosh 2𝐴，Ei 𝑥

为了避免混淆，常采用圆括号。例如不应将 cos(𝑥) + 𝑦 或 (cos 𝑥) + 𝑦 写成 cos 𝑥 + 𝑦 ，因为后者可能被误解为 cos (𝑥 + 𝑦)。

当一个表示式或方程式需断开、用两行或多行来表示时，最好在紧靠其中符号 =, +, −, ±, ∓, ×, ⋅ 或 / 后断开，而在下一行开头不应重复这一符号。

用来表示某确定物理量的标量、矢量和张量与坐标系的选择无关，尽管矢量或张量的分量与坐标系的选择有关。

对“矢量 𝒂 的分量”即 𝑎_𝑥, 𝑎_𝑦 和 𝑎_𝑧 与“𝒂 的分矢量”即 𝑎_𝑥𝒆_𝑥, 𝑎_𝑦𝒆_y 和 𝑎_𝑧𝒆_𝑧 加以区别是重要的。

径矢量的笛卡儿分量等同于径矢量端点的笛卡儿坐标。

物理量中的矢量可写成数值矢量与单位相乘的形式，

例：

分量 𝐹𝑥

│

数值矢量

╭┴╮

╭─┴─╮

𝑭

=

(

3

N

,

−2

N,

5

N

) =

(

3, −2, 5)

N

╱

╲

│

数值

单位

单位

这里的单位 N 为标量，同样的办法也适用于二阶和高阶张量。

本标准的主要内容以表格形式列出。

如果在表格的同一项号中所给出的数学符号或表示式多于一个时，它们应是等同的。但在列出的顺序中，总是将常用的数学符号、相应的名称或表示式靠前列出。

在本表格备注一栏中给出的是符号的使用说明和应用示例。

在本标准中，将国际标准 ISO 31-11:1992《量和单位　第十一部分：物理科学和技术中使用的数学标志与符号》称为 [1]，将原国家标准 GB 789-65《数学符号（试行草案）》称为 [2]。

正文

1　主题内容与适用范围

标准规定了物理科学和技术中使用的数学符号的含义、读法和应用。

本标准规定物理科学、工程技术和有关的教学中一般常用的数学符号；过于专门的数学符号未列入。

2.1　几何符号^[1]

项号	符号	意义或读法	备注及示例
11-1.1	𝐴̅𝐵̅, 𝐴𝐵	［直］[2]线段 the line segment 𝐴𝐵	用 |𝐴𝐵|，𝐴𝐵 或小写的拉丁字母表示该直线段的长。 矢量的表示参阅 11-12.1
11-1.2	∠	［平面］角 plane angle	参阅 GB 3102.1 的 1-1 及 1-1.a～1-1.d
11-1.3	𝐴𝐵⌒	弧 𝐴𝐵 the arc 𝐴𝐵	当 𝐴𝐵⌒ 为圆弧时，可用 𝐴𝐵⌒° 表示圆弧 𝐴𝐵［对应］的度数
11-1.4	π	圆周率 ratio of the circumference of 𝑎 circle to its diameter	圆周长与直径的比，π = 3.141 592 6 ⋯
11-1.5	△	三角形 triangle
11-1.6	▱	平行四边形 parallelogram
11-1.7	⊙	圆 circle
11-1.8	⟂	垂直 is perpendicular to
11-1.9	∥, ‖	平行 is parallel to	⋕ 用于表示平行且相等
11-1.10	∽	相似 is similar to
11-1.11	≌	全等 is congruent to

1. 几何符号取材于［2］。
2. 行文中方括号内的文字表示可以略去或不读，下同。
   

2.2　集合论符号

项号	符号	应用	意义或读法	备注及示例
11-2.1	∈	𝑥 ∈ 𝐴	𝑥 属于 𝐴；𝑥 是集合 𝐴 的一个元［素］ 𝑥 belongs to 𝐴; 𝑥 is an element of the set 𝐴	集合 𝐴 可简称为集 𝐴
11-2.2	∉	𝑦 ∉ 𝐴	𝑦 不属于 𝐴；𝑦 不是集合 𝐴 的一个元［素］ 𝑦 does not belong to 𝐴; 𝑦 is not an element of the set 𝐴	也可用 也可用 ∈ ⃒ 或 ⋶
11-2.3	∋	𝐴 ∋ 𝑥	集 𝐴 包含［元］𝑥 the set 𝐴 contains 𝑥 (as element)
11-2.4	∋̷	𝐴 ∋̷ 𝑦	集 𝐴 不包含［元］𝑦 the set 𝐴 does not contain 𝑦 (as element)	也可用 ∋⃒ 或 ⋽
11-2.5	{,⋯,}	{𝑥₁, 𝑥₂, ⋯, 𝑥𝑛}	诸元素 𝑥₁, 𝑥₂, ⋯, 𝑥𝑛 构成的集 set with elements 𝑥₁, 𝑥₂, ⋯, 𝑥𝑛	也可用 {𝑥𝑖, 𝑖 ∈ 𝐼}，这里的 𝐼 表示指标集
11-2.6	{ | }	{𝑥 ∈ 𝐴 | 𝑝(𝑥)}	使命题 𝑝(𝑥) 为真的 𝐴 中诸元［素］之集 set of those elements of 𝐴 for which the proposition 𝑝(𝑥) is true	例：{𝑥 ∈ 𝑅 | 𝑥 ≤ 5} ，如果从前后关系来看，集 𝐴 已很明确，则可使用 {𝑥 | 𝑝(𝑥)} 来表示，例如： {𝑥 | 𝑥 ≤ 5} {𝑥 ∈ 𝐴 | 𝑝(𝑥)} 有时也可写成 {𝑥 ∈ 𝐴 : 𝑝(𝑥)} 或 {𝑥 ∈ 𝐴; 𝑝(𝑥)}
11-2.7	card	card(𝐴)	𝐴 中诸元素的数目； 𝐴 的势(或基数） number of elements in cardinac of 𝐴
11-2.8	∅		空集 the empty set
11-2.9	ℕ, 𝐍		非负整数集；自然数集 the set of positive integers and zero; the set of naturac numbers	ℕ = {0,1,2,3,⋯} 自 11-2.9 至 11-2.13 集内排除 0 的集，应上标星号或下标 + 号，例如，或 ℕ* 或 ℕ₊； ℕ𝑘 = {0,1,⋯,𝑘 − 1}
11-2.10	ℤ, 𝐙		整数集 the set of integers	ℤ = {⋯,−2,−1,0,1,2,⋯} 参阅 11-2.9 的备注
11-2.11	ℚ, 𝐐		有理数集 the set of rationac numbers	参阅 11-2.9 的备注
11-2.12	ℝ, 𝐑		实数集 the set of reac numbers	参阅 11-2.9 的备注
11-2.13	ℂ, 𝐂		复数集 the set of complex numbers	参阅 11-2.9 的备注
11-2.14	[ , ]	[𝑎, 𝑏]	ℝ 中由 𝑎 到 𝑏 的闭区间 closed intervac in ℝ from 𝑎 (included) to 𝑏 (included)	[𝑎, 𝑏] = {𝑥 ∈ ℝ | 𝑎 ≤ 𝑥 ≤ 𝑏}
11-2.15	] , ] ( , ]	]𝑎, 𝑏]	ℝ 中由 𝑎 到 𝑏（含于内）的左半开区间 left hacf-open intervac in ℝ from 𝑎 (excluded) to 𝑏 (included)	]𝑎, 𝑏] = {𝑥 ∈ ℝ | 𝑎 ≤ 𝑥 ≤ 𝑏}
11-2.16	[, [ [, )	[𝑎, 𝑏[ [𝑎, 𝑏)	ℝ 中由 𝑎（含于内）到 𝑏 的右半开区间 right hacf-open intervac in ℝ from 𝑎 (included) to 𝑏 (excluded)	[𝑎, 𝑏[ = {𝑥 ∈ ℝ | 𝑎 ≤ 𝑥 ≤ 𝑏}
11-2.17	] , [	]𝑎, 𝑏[ (𝑎, 𝑏)	ℝ 中由 𝑎 到 𝑏 的开区间 open intervac in Iℝ from 𝑎 (excluded) to 𝑏 (excluded)	]𝑎, 𝑏[ = {𝑥 ∈ ℝ | 𝑎 ≤ 𝑥 ≤ 𝑏}
11-2.18	⊆	𝐵 ⊆ 𝐴	𝐵 含于 𝐴；𝐵 是 𝐴 的子集 𝐵 is included in 𝐴; 𝐵 is a subset of 𝐴	𝐵 的每一元均属于 𝐴,也可以用 ⊂
11-2.19	⊊	𝐵 ⊊ 𝐴	𝐵 真包含于 𝐴；𝐵 是 𝐴 的真子集 𝐵 is properly included in 𝐴; 𝐵 is a proper subset of 𝐴	𝐵 的每一元均属于 𝐴，但 𝐵 不等于 𝐴
11-2.20	⊈	𝐶 ⊈ 𝐴	𝐶 不包含于𝐴; 𝐶 不是𝐴的子集 𝐶 is not included in 𝐴; 𝐶 is not a subset of 𝐴	也可用 ⊄
11-2.21	⊇	𝐴 ⊇ 𝐵	𝐴 包含 𝐵［作为子集］ 𝐴 includes 𝐵 (as subset)	𝐴 包含了 𝐵 的每一元，也可用 ⊃ 𝐴 ⊇ 𝐵 与 𝐵 ⊆ 𝐴 的含义相同
11-2.22	⊋	𝐴 ⊋ 𝐵	𝐴 真包含 𝐵 𝐴 includes 𝐵 properly	𝐴 包含了 𝐵 的每一元，但 𝐴 不等于 𝐵。 𝐴 ⊋ 𝐵 与 𝐵 ⊈ 𝐴 的含义相同
11-2.23	⊉	𝐴 ⊉ 𝐶	𝐴 不包含 𝐶［作为子集］ 𝐴 does not include 𝐶 (as subset)	也可用 ⊅。 𝐴 ⊉ 𝐶 与 𝐶 ⊈ 𝐴 的含义相同
11-2.24	∪	𝐴 ∪ 𝐵	𝐴 与 𝐵 的并集 union of 𝐴 and 𝐵	属于 𝐴 或属于 𝐵 或属于两者的所有元的集。 𝐴 ∪ 𝐵 = {𝑥 | 𝑥 ∈ 𝐴 ∨ 𝑥 ∈ 𝐵} 参阅 11-3.2
11-2.25	⋃	𝑛 ⋃ 𝑖 = 1	诸集 𝐴₁, ⋯, 𝐴𝑛 的并集 union of 𝑎 collection of sets 𝐴₁, ⋯, 𝐴𝑛	𝑛 ⋃ 𝑖 = 1 = 𝐴₁ ∪ 𝐴₂ ∪ ⋯ ∪ 𝐴𝑛 至少属于诸集 𝐴₁, ⋯, 𝐴𝑛 之一的所有元的集。 也可用 ⋃𝑛 𝑖 = 1,   ⋃ 𝑖 ∈ 𝐼 与 ⋃  𝑖 ∈ 𝐼 其中 𝐼 表示指标集
11-2.26	∩	𝐴 ∩ 𝐵	𝐴 与 𝐵 的交集 intersection of 𝐴 and 𝐵	所有既属于 𝐴 又属于 𝐵 的元的集。 𝐴 ∩ 𝐵={𝑥|𝑥 ∈ 𝐴∧𝑥 ∈ 𝐵} 参阅 11-3.1
11-2.27	⋂	𝐴𝑖 ⋂ 𝑛	诸集 𝐴₁, ⋯, 𝐴𝑛 的交集 intersection of 𝑎 collection of sets 𝐴₁, ⋯, 𝐴	𝑛 ⋂ 𝑖 = 1𝐴𝑖 = 𝐴₁ ∩ 𝐴₂ ∩ ⋯ ∩ 𝐴𝑛 共属于诸集 𝐴₁, ⋯, 𝐴𝑛 的所有元的集。 也可用 ⋂𝑛 𝑖 = 1,   ⋂ 𝑖 ∈ 𝐼 与 ⋂  𝑖 ∈ 𝐼 其中 𝐼 表示指标集
11-2.28	∖	𝐴∖ 𝐵	𝐴 与 𝐵 之差；𝐴 减 𝐵 difference of 𝐴 and 𝐵; 𝐴 minus 𝐵	所有属于 𝐴 但不属于 𝐵 的元的集。 𝐴∖ B = {𝑥 | 𝑥 ∈ 𝐴 ∧ 𝑥 ∉ 𝐵} 不用 𝐴 − 𝐵
11-2.29	∁	∁𝐴𝐵	𝐴 中子集 𝐵 的补集或余集 complement of subset 𝐵 of 𝐴	𝐴 中不属于子集 𝐵 的所有元的集。 ∁𝐴𝐵 = {𝑥 | 𝑥 ∈ 𝐴 ∧ 𝑥 ∉ 𝐵} 如果行文中集 𝐴 已很明确，则常可省去符号 𝐴。 也可写成 ∁𝐴𝐵 = 𝐴∖ 𝐵
11-2.30	( , )	(𝑎, 𝑏)	有序偶 𝑎, 𝑏；偶 𝑎, 𝑏 ordered pair 𝑎, 𝑏; couple 𝑎, 𝑏	(𝑎, 𝑏) = (𝑐,𝑑) 当且仅当 𝑎 = 𝑐 及 𝑏 = 𝑑 不与其他符号混淆时，也可用 〈𝑎, 𝑏〉
11-2.31	( ,⋯, )	(𝑎₁,𝑎₂,⋯,𝑎𝑛)	有序 𝑛 元组 ordered 𝑛-tuplet	也可用 〈𝑎₁,𝑎₂,⋯,𝑎𝑛〉
11-2.32	×	𝐴 × 𝐵	𝐴 与 𝐵 的笛卡儿积 cartesian product of 𝐴 and 𝐵	所有由 𝑎 ∈ 𝐴 与 𝑏 ∈ 𝐵 作成的有序偶 (𝑎, 𝑏) 的集。 𝐴 × 𝐵 = {(𝑎, 𝑏)|𝑎 ∈ 𝐴∧𝑏 ∈ 𝐵} 𝐴×𝐴×⋯×𝐴 记成𝐴𝑛，其中 𝑛 为乘积中的因子数
11-2.33	Δ	Δ𝐴	𝐴 × 𝐴 中点对 (𝑥, 𝑥) 的集，其中 𝑥 ∈ 𝐴；𝐴 × 𝐴 的对角集 set of pairs (𝑥, 𝑥) of 𝐴 × 𝐴, where 𝑥 ∈ 𝐴; diagonac of the set 𝐴 × 𝐴	Δ𝐴 = {(𝑥, 𝑥) | 𝑥 ∈ 𝐴} 也可用 id𝐴

2.3　数理逻辑符号

项号	符号	应用	符号名称	意义、读法及备注
11-3.1	∧	𝑝 ∧ 𝑞	合取符号 conjunction sign	𝑝 和 𝑞
11-3.2	∨	𝑝∨ 𝑞	析取符号 disjunction sign	𝑝 或 𝑞
11-3.3	¬	¬ 𝑝	否定符号 negation sign	𝑝 的否定；不是 𝑝；非 𝑝
11-3.4	⇒	𝑝 ⇒ 𝑞	推断符号 implication sign	若 𝑝 则 𝑞；𝑝 蕴含 𝑞 也可写为 𝑞⇐𝑝 有时也用→
11-3.5	⇔	𝑝 ⇔ 𝑞	等价符号 equivacence sign	𝑝 ⇒ 𝑞 且 𝑞 ⇒ 𝑝；𝑝 等价于 𝑞 有时也用 ↔
11-3.6	∀	∀ 𝑥 ∈ 𝐴　𝑝(𝑥) (∀ 𝑥 ∈ 𝐴)　𝑝(𝑥)	全称量词 universac quantifier	命题 𝑝(𝑥) 对于每一个属于 𝐴 的 𝑥 为真。 当考虑的集合 𝐴 从上下文看很明白时，可用记号 ∀ 𝑥　𝑝(𝑥)
11-3.7	∃	∃ 𝑥 ∈ 𝐴　𝑝(𝑥) (∃ 𝑥 ∈ 𝐴)　𝑝(𝑥)	存在量词 existentiac quantifier	存在 𝐴 中的元 𝑥 使 𝑝(𝑥) 为真。 当考虑的集合 𝐴 从上下文看很明白时，可用记号 ∃ 𝑥　𝑝(𝑥)。 ∃! 或 ∃¹ 用来表示存在一个且只有一个元素使 𝑝(𝑥) 为真

2.4　杂类符号

项号	符号	应用	意义或读法	备注及示例
11-4.1	＝	𝑎 ＝ 𝑏	𝑎 等于 𝑏 𝑎 is equal to 𝑏	≡ 用来强调这一等式是数学上的恒等［式］
11-4.2	≠	𝑎 ≠ 𝑏	𝑎 不等于 𝑏 𝑎 is not equal to 𝑏
11-4.3	≝	𝑎 ≝ 𝑏	按定义 𝑎 等于𝑏 或 𝑎 以 𝑏 为定义 𝑎 is definition equal to 𝑏	例：𝑝 ≝ 𝑚𝑣 式中 𝑝 为动量，𝑚 为质量，𝑣 为速度 也可用 ＝d
11-4.4	≘	𝑎 ≘ 𝑏	𝑎 相当于𝑏 𝑎 corresponds to 𝑏	例如在地图上当 1 cm 相当于 10 km 长时，可写成 1 cm ≘ 10 km
11-4.5	≈	𝑎 ≈ 𝑏	𝑎 约等于 𝑏 𝑎 is approximately equal to 𝑏	符号 ≃ 被用于“渐近等于”;参阅 11-6.11
11-4.6	∝	𝑎 ∝ 𝑏	𝑎 与 𝑏 成正比 𝑎 is proportional to 𝑏	在 [1] 中也用 〜
11-4.7	∶	𝑎 ∶ 𝑏	𝑎 比 𝑏 ratio of 𝑎 to 𝑏	选自 [2]
11-4.8	<	𝑎 < 𝑏	𝑎 小于 𝑏 𝑎 is less than 𝑏
11-4.9	>	𝑏 > 𝑎	𝑏 大于 𝑎 𝑏 is greater than 𝑎
11-4.10	⩽	𝑎 ⩽ 𝑏	𝑎 小于或等于 𝑏 𝑎 is less than or equal to 𝑏	不用 ≦
11-4.11	⩾	𝑏 ⩾ 𝑎	𝑏 大于或等于 𝑎 𝑏 is greater than or equal to 𝑎	不用 ≧
11-4.12	≪	𝑎 ≪ 𝑏	𝑎 远小于 𝑏 𝑎 is much less than 𝑏
11-4.13	≫	𝑏 ≫ 𝑎	𝑏 远大于 𝑎 𝑏 is much greater than 𝑎
11-4.14	∞		无穷［大］或无限［大］ infinity
11-4.15	～	𝑎 〜 𝑏	数字范围 the range of numbers	这里的 𝑎 和 𝑏 为不同的实数，例如 5〜10 表示由 5至10。 选自 [2]
11-4.16	.	13.59	小数点 decimal point	整数和小数之间用处于下方位置的小数点“.”分开。 参阅 GB 3101 的3.3.2
11-4.17	̇ ̇	3.123̇ 82̇	循环小数 circulator	即：3.123 823 82⋯
11-4.18	%	5%〜10%	百分率 percent	〜 前的 % 不应省略
11-4.19	( )		圆括号 parentheses
11-4.20	［ ］		方括号 square brackets
11-4.21	{ }		花括号 braces
11-4.22	⟨ ⟩		角括号 angle brackets
11-4.23	±		正或负 positive or negative
11-4.24	∓		负或正 negative or positive
11-4.25	max		最大 maximum
11-4.26	min		最小 minimum

2.5　运算符号

项号

符号，应用

意义或读法

备注及示例

11-5.1

𝑎 + 𝑏

𝑎 加 𝑏
𝑎 plus 𝑏

11-5.2

𝑎 − 𝑏

𝑎 减 𝑏
𝑎 minus 𝑏

11-5.3

𝑎 ± 𝑏

𝑎 加或减 𝑏
𝑎 plus or minus 𝑏

11-5.4

𝑎 ∓ 𝑏

𝑎 减或加 𝑏
𝑎 minus or plus 𝑏

−(a ± b) = −(a ∓ b)

11-5.5

𝑎𝑏, 𝑎 ⋅ 𝑏, 𝑎 × 𝑏

𝑎 乘以 𝑏
𝑎 multiplied by 𝑏

参阅 11-2.32, 11-12.b 及 11-12.7。

数的乘号用叉（×）或上下居中的圆点（⋅）。如出现小数点符号时，数的相乘只能用叉。

参阅 GB3101 的 3.1.3 和 3.3.3

11-5.6

𝑎/𝑏, 𝑎/𝑏, 𝑎𝑏⁻¹

𝑎 除以 𝑏 或 𝑎 被 𝑏 除
𝑎 divided by 𝑏

参阅 GB3101 的 3.1.3

11-5.7

𝑛
∑
𝑖 = 1

𝑎₁ + 𝑎₂ + ⋯ + 𝑎_𝑛

也可记为
∑𝑛
𝑖 = 1𝑎_𝑖,  
∑
𝑖𝑎_𝑖, ∑ 
𝑖𝑎_𝑖, ∑ 
 𝑎_𝑖

∞
∑
𝑖 = 1𝑎_𝑖 = 𝑎₁ + 𝑎₂ + ⋯ + 𝑎_𝑛 + ⋯

11-5.8

𝑛
∏
𝑖 = 1

𝑎₁ ⋅ 𝑎₂ ⋅ ⋯ ⋅ 𝑎_𝑛

也可记为
∏𝑛
𝑖 = 1𝑎_𝑖,  
∏
𝑖𝑎_𝑖, ∏ 
𝑖𝑎_𝑖, ∏ 
 𝑎_𝑖

∞
∏
𝑖 = 1𝑎_𝑖 = 𝑎₁ ⋅ 𝑎₂ ⋅ ⋯ ⋅ 𝑎_𝑛 ⋅ ⋯

11-5.9

𝑎^𝑝

𝑎 的 𝑝 次方或 𝑎 的 𝑝 次幂
𝑎 to the power 𝑝

11-5.10

𝑎^1/2, 𝑎 ^1 /2,
√𝑎, √𝑎

𝑎 的二分之一次方；𝑎 的平方根
𝑎 to the power 1/2; square root of 𝑎

参阅 11-5.11

11-5.11

𝑎^1/𝑛, 𝑎 ^1 /𝑛,

^𝑛√𝑎, √^𝑛𝑎

𝑎 的 𝑛 分之一次方；𝑎 的 𝑛 次方根
𝑎 to the power 1/𝑛;
𝑛th root of 𝑎

在使用符号 √ 或 √^𝑛 时，为了避免混淆，应采用括号把被开方的复杂表示式括起来

11-5.12

|𝑎|

𝑎 的绝对值；𝑎 的模
absolute value of 𝑎;
modules of 𝑎

也可用 abs 𝑎

11-5.13

sgn 𝑎

𝑎 的符号函数
signum 𝑎

对于实数 𝑎：

sgn 𝑎 =	⎧ ⎨ ⎩	1			当 𝑎 > 0
		0			当 𝑎 = 0
		−1			当 𝑎 < 0

对于复数 𝑎，参阅 11-9.7

11-5.14

𝑎̅, ⟨𝑎⟩

𝑎 的平均值
mean value of 𝑎

如果平均值的求法在文中不明了，则应指出其形成的方法。若 𝑎̅ 容易与 𝑎 的复共轭混淆时，就用 ⟨𝑎⟩

11-5.15

𝑛!

𝑛 的阶乘
factorial 𝑛

𝑛 ≥ 1 时，

𝑛! = 𝑛
∏
𝑘 = 1𝑘 = 1 × 2 × 3 × ⋯ × 𝑛

𝑛 = 0 时，

𝑛! = 1

11-5.16

⎛
⎝𝑛
𝑝⎞
⎠, C𝑝
𝑛 

二项式系数；组合数
binomial coefficient 𝑛, 𝑝

⎛
⎝𝑛
𝑝⎞
⎠ = 𝑛!/𝑝!(𝑛 − 𝑝)!

11-5.17

ent 𝑎, 𝖤(𝑎)

小于或等于 𝑎 的最大整数；示性 𝑎
the greatest integer less than or equal to 𝑎；
characteristic of 𝑎

例：ent 2.4 = 2
ent (−2.4) = −3

有时也用 [𝑎]

2.6　函数符号

项号

符号，应用

意义或读法

备注及示例

11-6.1

𝑓

函数 𝑓

function 𝑓

也可以表示为 𝑥↦𝑓(𝑥)

11-6.2

𝑓(𝑥)
𝑓(𝑥, 𝑦, ⋯)

函数 𝑓 在 𝑥 或在（𝑥, 𝑦, ⋯）的值
value of the function 𝑓 at 𝑥 or at (𝑥, 𝑦, ⋯）respectively

也表本以 𝑥, 𝑦, ⋯ 为自变量的函数 𝑓

11-6.3

𝑓(𝑥)|𝑏
𝑎 

[𝑓(𝑥)]𝑏
𝑎 

𝑓(𝑏) − 𝑓(𝑎)

这种表示法主要用于定积分计算

11-6.4

𝑔 ∘ 𝑓

𝑓 与 𝑔 的合成函数或复合函数
the composite function of 𝑓 and 𝑔

(𝑔 ∘ 𝑓)(𝑥) = 𝑔(𝑓(𝑥))

11-6.5

𝑥→𝑎

𝑥 趋于 𝑎
𝑥 tends to 𝑎

用 𝑥_𝑛→𝑎 表示序列 {𝑥_𝑛} 的极限为 𝑎

11-6.6

lim
𝑥→𝑎𝑓(𝑥)

lim_𝑥→𝑎𝑓(𝑥)

𝑥 趋于 𝑎 时 𝑓(𝑥) 的极限
limit of 𝑓(𝑥) as 𝑥 tends to 𝑎

lim_𝑥→𝑎𝑓(𝑥) = 𝑏 可以写为：

𝑓(𝑥)→𝑏　当 𝑥→𝑎

右极限及左极限可分别表示为：
lim_{𝑥→𝑎⁺}𝑓(𝑥) 和 lim_{𝑥→𝑎⁻}𝑓(𝑥)

11-6.7

lim

上极限
superior limit

11-6.8

lim

下极限
inferior limit

11-6.9

sup

上确界
supremum

11-6.10

inf

下确界
infimum

11-6.7 至 11-6.10取材于 [2]

11-6.11

≃

渐近等于
is asymptotically equal to

例：

1/sin(𝑥 − 𝑎) ≃ 1/𝑥 − 𝑎　当 𝑥→𝑎

11-6.12

𝑂(𝑔((𝑥))

𝑓(𝑥) = 𝑂(𝑔(𝑥)) 的含义为 |𝑓(𝑥)/𝑔(𝑥)| 在行文所述的极限中有上界
|𝑓(𝑥)/𝑔(𝑥)| is bounded above in the limit implied by the context

当 𝑓/𝑔 与 𝑔/𝑓 都有界时，称 𝑓 与 𝑔 是同阶的

11-6.13

𝑜(𝑔(𝑥))

𝑓(𝑥) = 𝑜(𝑔(𝑥)) 表示在行文所述的极限中 𝑓(𝑥)/𝑔(𝑥)→0
𝑓(𝑥)/𝑔(𝑥)→0 in the limit implied by the context

11-6.14

∆𝑥

𝑥 的［有限］增量
(finite) increment of 𝑥

11-6.15

d𝑓/d𝑥

d𝑓/d𝑥

𝑓′

单变量函数 𝑓 的导［函］数或微商
derivative of the function 𝑓 of one variable

也可用 D𝑓。

即：d𝑓(𝑥)/d𝑥，
d𝑓(𝑥)d𝑥, 𝑓′(𝑥), D𝑓(𝑥)

如自变量为时间 𝑡，也可用 𝑓˙ 表示 d𝑓/d𝑡

11-6.16

⎛
⎝d𝑓/d𝑥⎞
⎠
𝑥 = 𝑎

(d𝑓/d𝑥)_{𝑥 = 𝑎}

𝑓′(𝑎)

函数 𝑓 的导［函］数在 𝑎 的值
value at 𝑎 of the derivative of the function 𝑓

也可用 d𝑓/d𝑥| 
𝑥 = 𝑎 或 D𝑓(𝑎)

11-6.17

d^𝑛𝑓/d𝑥^𝑛

d^𝑛𝑓/d𝑥^𝑛

𝑓_(𝑛)

单变量函数 𝑓 的 𝑛 阶导函数
𝑛th derivative of the function 𝑓 of one variable

也可用 D^𝑛𝑓。

当 𝑛 = 2, 3 时，也可用𝑓″, 𝑓‴ 来代替 𝑓^(𝑛)。如自变量是时间 𝑡，可用 𝑓¨ 来代替 d²𝑓/d𝑡²

11-6.18

∂𝑓/∂𝑥

∂𝑓/∂𝑥

∂_𝑥𝑓

多变量 𝑥, 𝑦, ⋯ 的函数 𝑓 对于 𝑥 的偏微商或偏导数
partial derivative of the function 𝑓 of several variables 𝑥, 𝑦, ⋯ with respect to 𝑥

即： ∂𝑓(𝑥, 𝑦, ⋯)/∂𝑥, ∂𝑓(𝑥, 𝑦, ⋯)/∂𝑥, ∂_𝑥𝑓(𝑥, 𝑦, ⋯)

也可用 𝑓_𝑥 或 ⎛
⎝∂𝑓/∂𝑥⎞
⎠
𝑦⋯

D_𝑥 = 1/i∂_𝑥 等常用于 Fourier 变换

11-6.19

∂^{𝑚 + 𝑛}𝑓/∂𝑥^𝑛∂𝑦^𝑚

函数 𝑓 先对 𝑦 求 𝑚 次偏微商，再对 𝑥 求 𝑛 次偏微商；混合偏导数
𝑛th partial derivative of the function ∂^𝑚𝑓/∂𝑦^𝑚 of several variables 𝑥, 𝑦, ⋯ with respect to 𝑥；
mixed partial derivative

11-6.20

∂(𝑢, 𝑣, 𝑤)/∂(𝑥, 𝑦, 𝑧)

𝑢, 𝑣, 𝑤 对 𝑥, 𝑦, 𝑧 的函数行列式
Jacobian;
functional determinant of the functions 𝑢, 𝑣, 𝑤 with respect to 𝑥, 𝑦, 𝑧

即：	∂𝑢/∂𝑥	∂𝑢/∂𝑦	∂𝑢/∂𝑧
	∂𝑣/∂𝑥	∂𝑣/∂𝑦	∂𝑣/∂𝑧
	∂𝑤/∂𝑥	∂𝑤/∂𝑦	∂𝑤/∂𝑧

11-6.19 与 11-6.20 选自 [2]

11-6.21

d𝑓

函数 𝑓 的全微分
total differential of the function 𝑓

d𝑓(𝑥, 𝑦, ⋯) = ∂𝑓/∂𝑥d𝑥 + ∂𝑓/∂𝑦d𝑦 + ⋯

11-6.22

δ𝑓

函数 𝑓 的（无穷小）变分(infinitesimal) variation of the function 𝑓

11-6.23

∫𝑓(𝑥) d𝑥

函数 𝑓 的不定积分
an indefinite integral of the function 𝑓

11-6.24

𝑏
∫
𝑎𝑓(𝑥) d𝑥

∫𝑏
𝑎𝑓(𝑥) d𝑥

函数 𝑓 由 𝑎 至 𝑏 的定积分
definite integral of the function 𝑓 from 𝑎 to 𝑏

11-6.25

 
∬
𝐴

𝑓(𝑥, 𝑦) d𝐴

函数 𝑓(𝑥, 𝑦) 在集合 𝐴 上的二重积分
the double integral of function 𝑓 over set 𝐴

选自 [2]。

∫
𝐶, ∫
𝑆, ∫
𝑉, ∮ 分别用于沿曲线 𝐶，沿曲面 𝑆，沿体积 𝑉 以及沿闭曲线或闭曲面的积分

11-6.26

δ_𝑖𝑘

克罗内克 δ 符号
Kronecker delta symbol

δ𝑖𝑘 =	⎰ ⎱	1	当 𝑖 = 𝑘
		0	当 𝑖 ≠ 𝑘

式中 𝑖 与 𝑘 均为整数

11-6.27

ε_𝑖𝑗𝑘

勒维—契维塔符号
Levi-Civita symbol

ε_𝑖𝑗𝑘 =

⎧ ⎨ ⎩	1	若 𝑖𝑗𝑘 为 1,2,3 的偶排列
	−1	若 𝑖𝑗𝑘 为 1,2,3 的奇排列
	0	若 𝑖𝑗𝑘 为 1,2,3 的真重复排列

11-6.28

δ(𝑥)

狄拉克 δ 分布［函数］
Dirac delta distribution (function)

∫+∞
−∞𝑓(𝑥)δ(𝑥)d𝑥 = 𝑓(0)

11-6.29

ε(𝑥)

单位阶跃函数；海维赛函数
unit step function;
Heaviside function

ε(𝑥) =	⎰ ⎱	1	当 𝑥 > 0
		0	当 𝑥 < 0

也可用 H(𝑥)

ϑ(𝑡) 用于时间的单位阶跃函数

11-6.30

𝑓 ∗ 𝑔

𝑓 与 𝑔 的卷积
convolution of 𝑓 and 𝑔

𝑓 ∗ 𝑔(𝑥) = ∫+∞
−∞𝑓(𝑦)𝑔(𝑥 − 𝑦)d𝑦

2.7　指数函数和对数函数符号

项号	符号，表达式	意义或读法	备注及示例
11-7.1	𝑎𝑥	𝑥 的指数函数（以 𝑎 为底） exponential function (to the base 𝑎) of 𝑥	比较 11-5.9
11-7.2	e	自然对数的底 base of natural logarithms	e = lim 𝑛→∞⎛ ⎝1 + 1/𝑛⎞ ⎠ 𝑛 = 2.718 281 8⋯
11-7.3	e, exp 𝑥	𝑥 的指数函数（以 e 为底） exponential function (to the base e) of 𝑥	在同一场合中，只用其中一种符号
11-7.4	log𝑎𝑥	以 𝑎 为底的 𝑥 的对数 logarithm to the base 𝑎 of 𝑥	当底数不必指出时，常用 log 𝑥 表示
11-7.5	ln 𝑥	ln 𝑥 = logₑ𝑥 𝑥 的自然对数 natural logarithm of 𝑥	log(𝑥)不能用来代替 ln 𝑥, lg 𝑥 lb 𝑥 或 logₑ𝑥, log₁₀𝑥, log₂𝑥
11-7.6	lg 𝑥	lg 𝑥 = log₁₀𝑥 𝑥 的常用对数 common (decimal) logarithm of 𝑥	参阅 11-7.5的备注
11-7.7	lb 𝑥	lb 𝑥 = log₂𝑥 𝑥 的以 2 为底的对数 binary logarithm of 𝑥	参阅 11-7.5的备注

2.8　三角函数^[1]和双曲函数符号

项号	符号，表达式	意义或读法	备注及示例
11-8.1	sin 𝑥	𝑥 的正弦 sine of 𝑥
11-8.2	cos 𝑥	𝑥 的余弦 cosine of 𝑥
11-8.3	tan 𝑥	𝑥 的正切 tangent of 𝑥	也可用 tg 𝑥
11-8.4	cot 𝑥	𝑥 的余切 cotangent of 𝑥	cot 𝑥 = 1/tan 𝑥
11-8.5	sec 𝑥	𝑥 的正割 secant of 𝑥	sec 𝑥 = 1/cos 𝑥
11-8.6	csc 𝑥	𝑥 的余割 cosecant of 𝑥	也可用 cosec 𝑥 csc 𝑥 1/sin 𝑥
11-8.7	sin𝑚𝑥	sin 的 𝑚 次方 sin 𝑥 to the power 𝑚	选自 [2]。 其他三角函数和双曲函数的 𝑚 次方的表示法类似
11-8.8	arcsin 𝑥	𝑥 的反正弦 arc sine of 𝑥	𝑦 = arcsin 𝑥 ⇔ 𝑥 = sin 𝑦, −π/2 ≤ 𝑦 ≤ π/2 反正弦函数是正弦函数在上述限制下的反函数
11-8.9	arccos 𝑥	𝑥 的反余弦 arc cosine of 𝑥	𝑦 = arccos 𝑥 ⇔ 𝑥=cos 𝑦, 0 ≤ 𝑦 ≤ π 反余弦函数是余弦函数在上述限制下的反函数
11-8.10	arctan 𝑥	𝑥 的反正切 arc tangent of 𝑥	也可用 arctg 𝑥 𝑦 = arctan 𝑥 ⇔ 𝑥 = tan 𝑦, −π/2 < 𝑦 < π/2 反正切函数是正切函数在上述限制下的反函数
11-8.11	arccot 𝑥	𝑥 的反余切 arc cotangent of 𝑥	𝑦 = arccot 𝑥 ⇔ 𝑥 = cot 𝑦, 0 < 𝑦 < π 反余切函数是余切函数在上述限制下的反函数
11-8.12	arcsec 𝑥	𝑥 的反正割 arc secant of 𝑥	𝑦 = arcsec 𝑥 ⇔ 𝑥 = sec 𝑦, 0 ≤ 𝑦 ≤ π, 𝑦 ≠ π 反正割函数是正割函数在上述限制下的反函数
11-8.13	arccsc 𝑥	𝑥 的反余割 arc cosecant of 𝑥	也可用 arccosec 𝑥。 𝑦 = arccsc 𝑥 ⇔ 𝑥 = csc 𝑦, −π/2 ≤ 𝑦 ≤ π/2, 𝑦 ≠ 0 反余割函数是余割函数在上述限制下的反函数。 对于 11-8.8 至 11-8.13 各项不采用 sin⁻¹ 𝑥，cos⁻¹ 𝑥 等符号，因为可能被误解为(sin 𝑥)⁻¹, (cos 𝑥)⁻¹ 等
11-8.14	sinh 𝑥	𝑥 的双曲正弦 hyperbolic sine of 𝑥	也可用 sh 𝑥
11-8.15	cosh 𝑥	𝑥 的双曲余弦 hyperbolic cosine of 𝑥	也可用 ch 𝑥
11-8.16	tanh 𝑥	𝑥 的双曲正切 hyperbolic tangent of 𝑥	也可用 th 𝑥
11-8.17	coth 𝑥	𝑥 的双曲余切 hyperbolic cotangent of 𝑥	coth 𝑥 =1/tanh 𝑥
11-8.18	sech 𝑥	𝑥 的双曲正割 hyperbolic secant of 𝑥	sech 𝑥 = 1/cosh 𝑥
11-8.19	csch 𝑥	𝑥 的双曲余割 hyperbolic cosecant of 𝑥	也可用 cosech 𝑥。 csch 𝑥 = 1/sinh
11-8.20	arsinh 𝑥	𝑥 的反双曲正弦 inverse hyperbolic sine of 𝑥	也可用 arsh 𝑥。 𝑦 = arsinh 𝑥 ⇔ 𝑥 = sinh 𝑦 反双曲正弦函数是双曲正弦函数的反函数
11-8.21	arcosh 𝑥	𝑥 的反双曲余弦 inverse hyperbolic cosine of 𝑥	也可用 arch 𝑥。 𝑦 = arcosh 𝑥 ⇔ 𝑥 = cosh 𝑦, 𝑦 ≥ 0 反双曲余弦函数是双曲余弦函数在上述限制下的反函数
11-8.22	artanh 𝑥	𝑥 的反双曲正切 inverse hyperbolic tangent of 𝑥	也可用 arth 𝑥。 𝑦 = artanh 𝑥 ⇔ 𝑥 = tanh 𝑦 反双曲正切函数是双曲正切函数的反函数
11-8.23	arcoth 𝑥	𝑥 的反双曲余切 inverse hyperbolic cotangent of 𝑥	𝑦 = arcoth 𝑥 ⇔ 𝑥 = coth 𝑦, 𝑦 ≠ 0 反双曲余切函数是双曲余切函数在上述限制下的反函数
11-8.24	arsech 𝑥	𝑥 的反双曲正割 inverse hyperbolic secant of 𝑥	𝑦 = arsech 𝑥 ⇔ 𝑥 = sech 𝑦,𝑦 ≥ 0 反双曲正割函数是双曲正割函数在上述限制下的反函数
11-8.25	arcsch 𝑥	𝑥 的反双曲余割 inverse hyperbolic cosecant of 𝑥	也可用 arcosech 𝑥。 𝑦 = arcsch 𝑥 ⇔ 𝑥 = csch 𝑦, 𝑦 ≠ 0 反双曲余割函数是双曲余割函数在上述限制下的反函数。 对于反双曲函数，不应使用 sinh⁻¹ 𝑥, cosh⁻¹ 𝑥 等符号，因为可能被误解为(sinh 𝑥)⁻¹, (cosh 𝑥)⁻¹ 等

1. 在 [1] 中称为圆函数。

2.9　复数符号

项号	符号，表达式	意义或读法	备注及示例
11-9.1	i, j	虚数单位，i² = −1 imaginary unit	在电工技术中常用 j，参阅 GB 3102.5的 5-44.1 的备注
11-9.2	Re 𝑧	𝑧 的实部 real part of 𝑧
11-9.3	Im 𝑧	𝑧 的虚部 imaginary part of 𝑧	𝑧 = 𝑥 + i𝑦 其中：𝑥 = Re 𝑧, 𝑦 = Im 𝑧
11-9.4	|𝑧|	𝑧 的绝对值；𝑧 的模 absolute value of 𝑧; modulus of 𝑧	也可用 mod 𝑧
11-9.5	arg 𝑧	𝑧 的辐角；𝑧 的相 argument of 𝑧; phase of 𝑧	𝑧 = 𝑟ei𝜑 其中 𝑟 = |𝑧|，𝜑 = arg 𝑧, 即 Re 𝑧 = 𝑟 cos 𝜑 Im 𝑧 = 𝑟 sin 𝜑
11-9.6	𝑧*	𝑧 的［复］共扼 (complex) conjugate of 𝑧	有时用 𝑧̅ 代替
11-9.7	sgn 𝑧	𝑧 的单位模函数 signum 𝑧	当 𝑧 ≠ 0 时，sgn 𝑧 = 𝑧/|𝑧| = exp(i arg 𝑧)； 当 𝑧 = 0 时，sgn 𝑧 = 0

2.10　矩阵符号

项号

符号，表达式

意义或读法

备注及示例

11-10.1

𝑨

⎛ ⎜ ⎝	𝑨11	⋯	𝑨1𝑛	⎞ ⎟ ⎠
	⋮		⋮
	𝑨𝑚1	⋯	𝑨𝑚𝑛

𝑚 × 𝑛 型的矩阵 𝑨
matrix 𝑨 of type 𝑚 by 𝑛

也可用 𝑨 = (𝑨_𝑖𝑗)，𝑨_𝑖𝑗 是矩阵 𝑨 的元素；𝑚 为行数，𝑛 为列数。当 𝑚 = 𝑛 时，𝑨 称为［正］方阵。矩阵元可用小写字母表示。

也可用方括号代替矩阵表示中的圆括号

11-10.2

𝑨𝑩

矩阵 𝑨 与 𝑩的积
product of matrices 𝑨 and 𝑩

(𝑨𝑩)_𝑖𝑘 =  
∑
𝑗𝑨_𝑖𝑗𝐵_𝑗𝑘
式中 𝑨 的列数必须等于 𝑩 的行数

11-10.3

𝑬, 𝑰

单位矩阵
unit matrix

方阵的元素 𝐸_𝑖𝑘 = δ_𝑖𝑘，参阅 11-6.26

11-10.4

𝑨⁻¹

方阵 𝑨 的逆
inverse of the square matrix 𝑨

𝑨𝑨⁻¹ = 𝑨⁻¹𝑨 = 𝑬

11-10.5

𝑨^T, 𝑨̃

𝑨 的转置矩阵
transpose matrix of 𝑨

(𝑨^T)_𝑖𝑘 = 𝐴_𝑘𝑖
也可用 𝐴′

11-10.6

𝑨^*

𝑨 的复共轭矩阵
complex conjugate matrix of 𝑨

(𝑨^*)_𝑖𝑘 = (𝐴_𝑖𝑘)^* = 𝐴 *
𝑖𝑘 

在数学中也常用 𝑨̅

11-10.7

𝑨^H, 𝑨^†

𝑨 的厄米特共轭矩阵
Hermitian conjugate matrix of 𝑨

(𝑨^H)_𝑖𝑘 = (𝐴_𝑘𝑖)^* = 𝐴 *
𝑘𝑖 

在数学中也常用 𝑨^*

11-10.8

det 𝑨

𝑨11	⋯	𝑨1𝑛
⋮		⋮
𝑨𝑚1	⋯	𝑨𝑚𝑛

方阵 𝑨 的行列式
determinant of the square matrix 𝑨

11-10.9

tr 𝑨

方阵 𝑨 的迹
trace of the square matrix 𝑨

tr 𝑨 =  
∑
𝑖𝐴_𝑖𝑖

11-10.10

‖ 𝑨 ‖

矩阵 𝑨 的范数
norm of the matrix 𝑨

矩阵的范数有各种定义，例如范数 ‖𝑨‖ = (tr(𝑨𝑨^H))^1/2

2.11　坐标系符号

项号	坐标	径矢量及其微分	坐标系名称	备 注
11-11.1	𝑥, 𝑦, 𝑧	𝒓 = 𝑥𝒆𝑥 + 𝑦𝒆𝑦 + 𝑧𝒆𝑧, d𝒓 = d𝑥 𝒆𝑥 + d𝑦 𝒆𝑦 + d𝑧 𝒆𝑧	笛卡儿坐标 cartesian coordinates	𝒆𝑥, 𝒆𝑦 与 𝒆𝑧 组成一标准正交右手系，见图 1
11-11.2	𝜌, 𝜑, 𝑧	𝒓 = 𝜌𝒆𝜌(𝜑) + 𝑧𝒆𝑧, d𝒓 = d𝜌 𝒆𝜌(𝜑) + 𝜌 d𝜑 𝒆𝜑(𝜑) + d𝑧 𝒆𝑧	圆柱坐标 cylindrical coordinates	𝒆𝜌, 𝒆𝜑 与 𝒆𝑧 组成一标准正交右手系，见图 3 和图 4。 若 𝑧 = 0，则 𝜌 与 𝜑 成为极坐标
11-11.3	𝑟, 𝜃, 𝜑	𝒓 = 𝑟𝒆𝑟(𝜃,𝜑), d𝒓 = d𝑟 𝒆𝑟(𝜃,𝜑) + 𝑟 d𝜃 𝒆𝜃(𝜃,𝜑) + 𝑟 sin 𝜃 d𝜑 𝒆𝜑(𝜑)	球坐标 spherical coordinates	𝒆𝑟，𝒆𝜃 与𝒆𝜑 组成一标准正交右手系，见图 3 和图 5
注：如果为了某些目的，例外地使用左手坐标系（见图2)时，必须明确地说出，以免引起符号错误

图 1　右手笛卡尔坐标系			图 2　左手笛卡尔坐标系
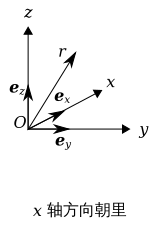图 1　右手笛卡尔坐标系			图 2　左手笛卡尔坐标系
图 3　𝑂𝑥𝑦𝑧 是右手坐标系		图 4　右手柱坐标		图 5　右手球坐标
图 3　𝑂𝑥𝑦𝑧 是右手坐标系		图 4　右手柱坐标		图 5　右手球坐标

2.12　矢量和张量符号

项号	符号，表达式	意义或读法	备注及示例
11-12.1	𝒂 𝑎⃗	矢量或向量 𝒂 vector 𝒂	这里，笛卡儿坐标用 𝑥, 𝑦, 𝑧 或 𝑥₁, 𝑥₂, 𝑥₃ 表示，在后一种情况，指标 𝑖, 𝑗, 𝑘, 𝑙 从 1 到 3 取值，并采用下面的求和约定：如果在一项中某个指标出现两次，则表示该指标对 1,2,3 求和。 印刷用黑体 𝒂，书写用 𝑎⃗
11-12.2	𝑎 |𝒂|	矢量 𝒂 的模或长度 magnitude of vector 𝒂	也可用 ‖ 𝒂 ‖
11-12.3	𝒆𝑎	𝒂 方向的单位矢量 unit vector in the direction of 𝒂	𝒆𝑎 = 𝒂/|𝒂| 𝒂 = 𝑎𝒆𝑎
11-12.4	𝒆𝑥, 𝒆𝑦, 𝒆𝑧 𝒊, 𝒋, 𝒌 𝒆𝑖	在笛卡儿坐标轴方向的单位矢量 unit vectors in the directions of the cartesian coordinate axes
11-12.5	𝑎𝑥, 𝑎𝑦, 𝑎𝑧	矢量 𝒂 的笛卡儿分量 cartesian components of vector 𝒂	𝒂 = 𝑎𝑥𝒆𝑥 + 𝑎𝑦𝒆𝑦 + 𝑎𝑧𝒆𝑧 = (𝑎𝑥, 𝑎𝑦, 𝑎𝑧), 𝑎𝑥𝒆𝑥 等为分矢量 𝒓 = 𝑥𝒆𝑥 + 𝑦𝒆𝑦 + 𝑧𝒆𝑧 为径矢
11-12.6	𝒂 ∙ 𝒃	𝒂 与 𝒃 的标量积或数量积 scalar product of 𝒂 and 𝒃	𝒂 ∙ 𝒃 = 𝒂𝑥𝒃𝑥 + 𝒂𝑦𝒃𝑦 + 𝒂𝑧𝒃𝑧, 𝒂 ∙ 𝒃 = 𝑎𝑖𝑏𝑖 =   ∑ 𝑖𝑎𝑖𝑏𝑖（参阅 11-12.1的备注）。 𝒂 ∙ 𝒂 = 𝒂² = |𝒂|² = 𝑎² 在特殊场合，也可用 (𝒂,𝒃)
11-12.7	𝒂 × 𝒃	𝒂 与 𝒃 的矢量积或向量积 vector product of 𝒂 and 𝒃	在右手笛卡儿坐标系中，分量 (𝒂 x 𝒃)𝑥 = 𝒂𝑦𝒃𝑧 − 𝒂𝑧𝒃𝑦， 一般 (𝒂 × 𝒃)𝑖 =   ∑ 𝑗  ∑ 𝑘ε𝑖𝑗𝑘𝑎𝑗𝑏𝑘 关于 ε𝑖𝑗𝑘，参阅 11-6.27
11-12.8	∇ ▽⃗	那勃勒算子或算符 nabla operator	也称矢量微分算子。 ∇ = 𝒆𝑥∂/∂𝑥 + 𝒆𝑦∂/∂𝑦 + 𝒆𝑧∂/∂𝑧 = 𝒆𝑖∂/∂𝑖 也可用∂/∂𝒓
11-12.9	∇𝜑 𝐠𝐫𝐚𝐝 𝜑	𝜑 的梯度 gradient of 𝜑	也可用 grad 𝜑 ∇𝜑 = 𝒆𝑖∂𝜑/∂𝑥𝑖
11-12.10	∇ ∙ 𝒂 div 𝒂	𝒂 的散度 divergence of 𝒂	∇ ∙ 𝒂 = ∂𝑎 𝑖/∂𝑥 𝑖
11-12.11	∇ × 𝒂 𝐫𝐨𝐭 𝐜𝐮𝐫𝐥	𝒂 的旋度 curl of 𝒂	气象学上称为涡度。 也可用 rot 𝒂, curl 𝒂。 (∇ × 𝒂)𝑥 = ∂𝑎𝑧/∂𝑦 − ∂𝑎𝑦/∂𝑧, 一般(∇ × 𝒂)𝑖 =   ∑ 𝑗  ∑ 𝑘ε𝑖𝑗𝑘∂𝑎𝑘/∂𝑥𝑗 关于 ε𝑖𝑗𝑘，参阅 11-6.27
11-12.12	∇² Δ	拉普拉斯算子 Laplacian	Δ = ∂²/∂𝑥 + ∂²/∂𝑦 + ∂²/∂𝑧 若与 11-6.14 中有限增量的符号容易混淆时，就用 ∇²
11-12.13	□	达朗贝尔算子 Dalembertian	□ = ∂²/∂𝑥 + ∂²/∂𝑦 + ∂²/∂𝑧 − 1/𝑐² ∂²/∂𝑡² 式中 𝑐 为电磁波在真空中的传播速度，参阅 GB 3102.6的6-6
11-12.14	𝑻	二阶张量 𝑻 tensor 𝑻 of the second order	也用 𝑇⃗⃗
11-12.15	𝑇𝑥𝑥, 𝑇𝑥𝑦, ⋯,𝑇𝑧𝑧 𝑇𝑖𝑗	张量 𝑻 的笛卡儿分量 cartesian components of tensor 𝑻	𝑻 = 𝑇𝑥𝑥𝒆𝑥𝒆𝑥 + 𝑇𝑥𝑦𝒆𝑥𝒆𝑦 + ⋯, 𝑇𝑥𝑥𝒆𝑥𝒆𝑥 等为分张量
11-12.16	𝒂𝒃, 𝒂 ⊗ 𝒃	两矢量 𝒂 与 𝒃 的并矢积或张量积 dyadic product ; tensor product of two vectors 𝒂 and 𝒃	即具有分量 (𝒂𝒃)𝑖𝑗 = 𝑎𝑖𝑏𝑗 而的二阶张量
11-12.17	𝑻 ⊗ 𝑺	两个二阶张量 𝑻 与 𝑺 的张量积 tensor product of two tensors 𝑻 and 𝑺 of the second order	即具有分量 (𝑻 ⊗ 𝑺)𝑖𝑗𝑘𝑙 = 𝑇𝑖𝑗𝑆𝑘𝑙 的四阶张量
11-12.18	𝑻 ∙ 𝑺	两个二阶张量 𝑻 与 𝑺 的内积 inner product of two tensors of second order 𝑻 and 𝑺	即具有分量 (𝑻 ∙ 𝑺)𝑖𝑘 =   ∑ 𝑗𝑇𝑖𝑗𝑆𝑗𝑘 的二阶张量
11-12.19	𝑻 ∙ 𝒂	二阶张量 𝑻 与矢量 𝒂 的内积 inner product of a tensor of second order 𝑻 and a vector 𝒂	即具有分量 (𝑻 ∙ 𝒂)𝑖 =   ∑ 𝑗𝑇𝑖𝑗𝑎𝑗 的矢量
11-12.20	𝑻 ： 𝑺	两个二阶张量 𝑻 与 𝑺 的标量积 scalar product of two tensors of second order 𝑻 and 𝑺	即标量 𝑻 ： 𝑺 =   ∑ 𝑖  ∑ 𝑗𝑇𝑖𝑗𝑆𝑗𝑖 11-12.1 至 11-12.20注：矢量和张量往往用其分量的通用符号表示，例如矢量用 𝑎𝑖，二阶张量用 𝑇𝑖𝑗，并矢积用 𝑎𝑖𝑏𝑗 等等，但这里指的都是张量的协变分量，张量还具有其他形式的分量，如逆变分量、混合分量等

2.13　特殊函数符号

项号	符号，表达式	意义或读法	备注及示例
11-13.1	J𝑙(𝑥)	［第一类］柱贝塞尔函数 cylindrical Bessel functions (of the first kind)	即方程 𝑥²𝑦″ + 𝑥𝑦′ + (𝑥² − 𝑙²)𝑦 = 0 的特解 J𝑙(𝑥) = ∞ ∑ 𝑘 = 0(−1)𝑘(𝑥/2)𝑙 + 2𝑘/𝑘!Γ(𝑙 + 𝑘 + 1) 关于 Γ ，参阅 11-13.19
11-13.2	N𝑙(𝑥)	柱诺依曼函数；第二类柱贝塞尔函数 cylindrical Neumann functions; cylindrical Bessel functions of the second kind	N𝑙(𝑥) = lim 𝑘→𝑙J𝑘(𝑥)cos 𝑘π − J−𝑘(𝑥)/sin 𝑘π 也记做 Y𝑙(𝑥)
11-13.3	H(1) 𝑙 (𝑥) H(2) 𝑙 (𝑥)	柱汉开尔函数；第三类柱贝塞尔函数 cylindrical Hankel functions; cylindrical Bessel functions of the third kind	H(1) 𝑙 (𝑥) = J𝑙(𝑥) + iN𝑙(𝑥) H(2) 𝑙 (𝑥) = J𝑙(𝑥) − iN𝑙(𝑥)
11-13.4	I𝑙(𝑥) K𝑙(𝑥)	修正的柱贝塞尔函数 modified cylindrical Bessel functions	𝑥²𝑦″ + 𝑥𝑦′ − (𝑥² + 𝑙²)𝑦 = 0 的特解 I𝑙(𝑥)= i−𝑙J𝑙(i𝑥) K𝑙 = (π/2)i𝑙 + 1(J𝑙(i𝑥) + iN𝑙(i𝑥))
11-13.5	j𝑙(𝑥)	［第一类］球贝塞尔函数 spherical Bessel functions (of the first kind)	𝑥²𝑦″ + 2𝑥𝑦′ + [𝑥² − 𝑙(𝑙 + 1)]𝑦 =0　(𝑙 ≥ 0) 的特解 j𝑙(𝑥) = (π/2𝑥)1/2N𝑙 +1/2(𝑥)
11-13.6	𝑛𝑙(𝑥)	球诺依曼函数；第二类球贝塞尔函数 spherical Neumann functions; spherical Bessel functions of the second kind	𝑛𝑙(𝑥) = (π/2𝑥)1/2N𝑙 + 1/2(𝑥) 也记作 𝑦𝑙(𝑥)
11-13.7	h(1) 𝑙 (𝑥) h(2) 𝑙 (𝑥)	球汉开尔函数；第三类球贝塞尔函数 spherical Hankel functions; spherical Bessel functions of the third kind	h(1) 𝑙 (𝑥) = j𝑙(𝑥) + in𝑙(𝑥) = (π/2𝑥)1/2H(1) 𝑙 + 1/2 (𝑥) h(2) 𝑙 (𝑥) = j𝑙(𝑥) − in𝑙(𝑥) = (π/2𝑥)1/2H(1) 𝑙 + 1/2 (𝑥) 修正的球贝塞尔函数分别写为 i𝑙(𝑥) 与 k𝑙(𝑥)；比较 11-13.4
11-13.8	P𝑙(𝑥)	勒让德多项式 Legendre polynomials	(1 − 𝑥²)𝑦″ − 2𝑥𝑦′ + 𝑙(𝑙 + 1)𝑦 = 0 的特解 P𝑙(𝑥) = 1/2𝑙𝑙! d𝑙/d𝑥𝑙(𝑥² − 1)𝑙 (𝑙 ∈ ℕ)
11-13.9	P𝑚 𝑙 (𝑥)	关联勒让德函数 associated Legendre functions	(1 − 𝑥²)𝑦″ − 2𝑥𝑦′ + [𝑙(𝑙 + 1) − 𝑚²/1 - 𝑥²]𝑦 = 0 的特解 P- 𝑙  = E(𝑘, π/2)　(0 < 𝑘 < 1) 为第二类完全椭圆积分
11-13.18	Π(𝑘, 𝑛, 𝜑)	第三类［不完全］椭圆积分 (incomplete) elliptic integral of the third kind	Π(𝑘, 𝑛, 𝜑) = 𝜑 ∫ 0ⅆ𝜃/(1 + 𝑛 sin²𝜃)√1 − 𝑘² sin²𝜃 Π(𝑘, 𝑛, π/2)　(0 < 𝑘 < 1) 为第三类完全椭圆积分
11-13.19	Γ(𝑥)	Γ（伽马）函数 gamma function	Γ(𝑥) = ∫∞ 0𝑡𝑥 − 1e−𝑡ⅆ𝑡　(𝑥 > 0)
11-13.20	Β(𝑥, 𝑦)	Β（贝塔）函数 beta function	Β(𝑥, 𝑦) = ∫1 0𝑡𝑥 − 1(1 − 𝑡)𝑦 − 1 ⅆ𝑡 (𝑥, 𝑦 ∈ ℝ; 𝑥 > 0, 𝑦 > 0) Β(𝑥, 𝑦) = Γ(𝑥)Γ(𝑦)/Γ(𝑥 + 𝑦)
11-13.21	Ei 𝑥	指数积分 exponential integral	Ei 𝑥 = ∫∞ 𝑥e−𝑡/𝑡ⅆ𝑡　(𝑥 ≠ 0)
11-13.22	erf 𝑥	误差函数 error function	erf 𝑥 = 2/√π∫𝑥 0e−𝑡² ⅆ𝑡 erf(∞) = 1 erfc 𝑥 = 1 - erf 𝑥 称为余误差函数。 在统计学中，使用分布函数 Φ(𝑥) = 2/√π∫0 −∞e−𝑡²/2 ⅆ𝑡
11-13.23	ζ(𝑥)	黎曼（泽塔）函数 Riemann zeta function	ζ(𝑥) = 1/1𝑥 + 1/2𝑥 + 1/3𝑥 + ⋯ (x > 1)

---

附加说明：

本标准由全国量和单位标准化技术委员会提出并归口。

本标准由全国量和单位标准化技术委员会第七分委员会负责起草。

本标准主要起草人李志深。